8. 2D Example
The nonstandard (NS) FDTD algorithm provides much higher accuracy than standard (S) FDTD one for the cylindrical Mie scattering.
Here we introduce Mie solutions in the TM and TE modes and compare numerical solutions of S- and NS-FDTD algorithms with the analytic.
Cylindrical Mie Scattering
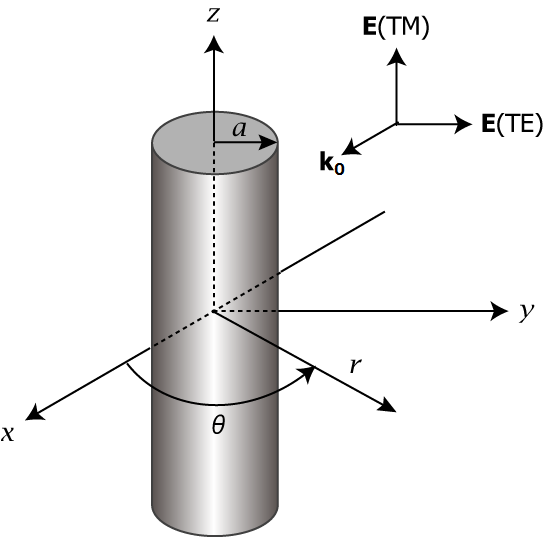
Fig. 1. Infinite plane wave impinging on an infinite dielectric cylinder (a = radius, k0 = wave vector in vacuum).
TH and TE polarizations are shown. Wave propagates along +x axis.
Maxwell's equations can be reduced to the Helmholtz equation for Ez,
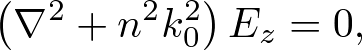 . . . (1)
where n is the refractive index and k0 is the wavenumber in vacuum.
This Helmholtz equation for an infinite cylinder shown in Fig. 1 is solved by Mie theory [1].
In the TM mode, Ez is independent of z so Ez = Ez(x, y).
Outside the cylinder, Ez is the sum of the incident field Ez0 = eik0x
and the outgoing scattered field Ezs. Taking (x, y) = r(cosθ, sinθ),
Ezs can be expanded in the form,
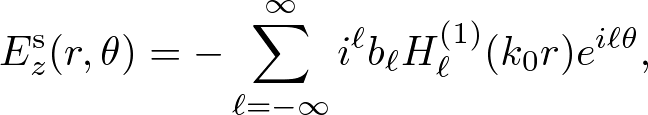 . . . (2)
where Hl(1) is the Hankel function of the first kind and the bl is the expansion coefficient to be determined.
The electric field inside the cylinder, Ezi, can be expanded in the form,
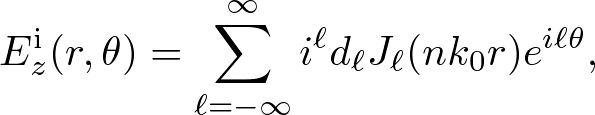 . . . (3)
where Jl is the Bessel function of the first kind and dl is the expansion coefficient.
The expansion coefficients, bl and dl, are determined by the physical conditions that
both Ez and its derivative ∂r must be continuous on the cylinder boundary. Using the fact that
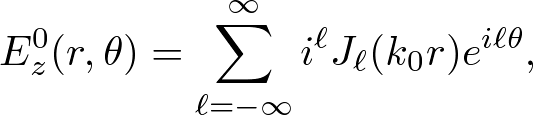 . . . (4)
we obtain
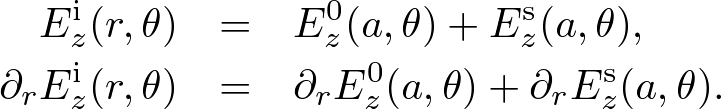 . . . (5)
Using the identity Z'l(x) = Zl-1(x) - (l/x)Zl(x) where Zl = Jl and Hl(1),
we can determine the expansion coefficients. Abbreviating x = k0a, we find
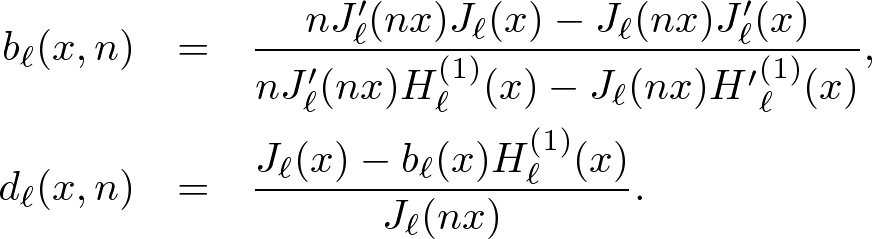 . . . (6)
In the TE mode, the incident polarization is defined by Er0 = eik0xsinθ and
Eθ0 = eik0xcosθ. Similarly, we obtain the outgoing scattered field,
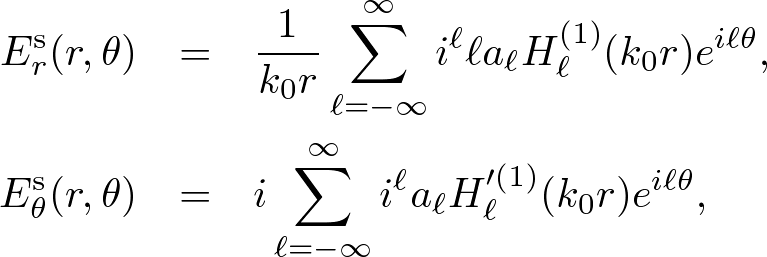 . . . (7)
and the electric field inside the cylinder is given by
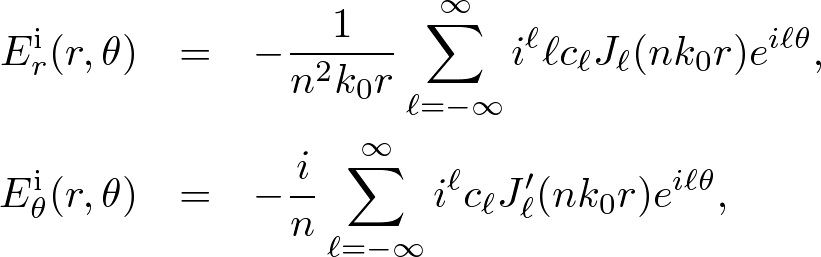 . . . (8)
where
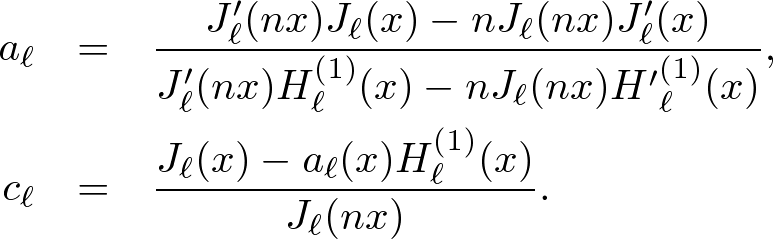 . . . (9)
The transform from polar coordinates to Cartesian ones is given by
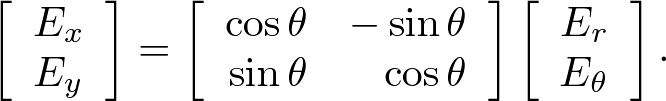 . . . (10) Example Simulation
Figure 2 is an example Mie scattering in the TM mode. The computational domain is terminated by 2nd-order Mur ABC.
Inside infinite cylinder consists of optical glass and outside is air.
Fig. 2. Example simulation of Mie scattering in the TM mode. Computational domain is 12μm×12μm and is terminated by 2nd-order Mur ABCs.
Inside infinite cylinder consists of optical glass and outside is air.
Simulation parameters are listed in Table 1.
Table. 1. Simulation parameters.
| Source wavelength λ |
Grid spaceing h |
| 1550nm |
150nm |
Since Maxwell's equations are equivalent to the wave equation in the TM mode, let us solve latter.
Because the NS-FDTD program can be easily reduced to the S-FDTD one, let us program the NS-FDTD simulation.
As below, we separate the program into FDTD computation and visualization parts.
FDTD Computation
We describe the two-dimensional NS-FDTD simulation class based on scattered field formulation in Source 1.
Source. 1. Two-dimensional FDTD calculation class. [Download Source 1]
// One-dimensional FDTD simulation
class FDTD2D {
private:
int Nx, Ny; // grid size
int num_elements; // number of grid points
double v; // wave speed
double h; // grid spacing
double dt; // time interval
double lambda; // wavelength
double k; // wavenumber
double omega; // angular frequency
double radius; // cylinder radius
double* psi_next; // next field
double* psi_current; // current field
double* psi_previous; // previous field
double* u; // coefficient matrix
double* n; // refractive index
double* gamma1; // gamma coefficient for NS-FDTD
double t; // simulation time
public:
// Initialization
void Initialize( void )
{
Nx = Ny = 12000/150; // grid size
num_elements = Nx * Ny; // number of grid points
h = 1; // grid spacing
dt = 1; // time interval
v = 0.7; // wave speed
lambda = 1550 / 150; // wavelength
k = 2*M_PI/lambda; // wavenumber
omega = v * k; // angular frequency
radius = 1500 / 150; // cylinder radius
// Get memory
psi_next = new double [num_elements];
psi_current = new double [num_elements];
psi_previous = new double [num_elements];
u = new double [num_elements];
n = new double [num_elements];
gamma1 = new double [num_elements];
// Set init field
for ( int i=0; i<num_elements; i++ ) {
// wave field
psi_next[i] = psi_current[i] = psi_previous[i] = 0;
}
// Set media distribution
FuzzyModel();
// Set u and gamma1
SetCoefficients();
}
// Finalize
void Finalize( void )
{
// Release memory
delete [] psi_next;
delete [] psi_current;
delete [] psi_previous;
delete [] u;
delete [] n;
delete [] gamma1;
}
// Get index
int idx( int i, int j )
{
return ( i*Ny + j );
}
// Set scatterer
bool IsInCircle( double x, double y, double r )
{
if ( x*x + y*y <= r*r ) return true;
else return false;
}
// Set Permittivity
void FuzzyModel()
{
// glass refractive index
double n_glass = 1.6;
for ( int i=0; i<Nx; i++ ) {
for ( int j=0; j<Ny; j++ ) {
// Get index
int id = idx( i, j );
// Get center
double cx = (Nx-1) / 2.0;
double cy = (Ny-1) / 2.0;
// Get position
double x = i - cx;
double y = j - cy;
// subgrid size
int subN = 20;
// Get areas
double area;
for ( int p=0; p<subN; p++ ) {
for ( int q=0; q<subN; q++ ) {
// Get shifted position
double sx = x - 0.5 + p/(double)(subN-1);
double sy = y - 0.5 + q/(double)(subN-1);
if ( IsInCircle( sx, sy, radius ) ) {
area += 1.0;
}
}
}
area /= (double)(subN*subN);
// Set permittivity by Fuzzy model
n[id] = sqrt( n_glass*n_glass*area + (1.0-area) );
}
}
}
// Set u and gamma1
void SetCoefficients()
{
for ( int i=0; i<Nx; i++ ) {
for ( int j=0; j<Ny; j++ ) {
// Get index
int id = idx( i, j );
// Set u
u[id] = sin(omega*dt/2) / sin(k*n[id]*h/2);
// Set gamma1
gamma1[id] = 1.0/6.0 + (k*n[id])*(k*n[id])*h*h*(
1.0/180.0 - (k*n[id])*(k*n[id])*h*h/23040.0 );
}
}
}
// Nonstandard Mur ABC
void nsMurABC( int i, int j )
{
double u1 = tan(omega*dt/2) / tan(k*h/2);
double th = M_PI / 3;
double u2 = 2*sin(omega*dt/2)*sin(omega*dt/2)
* ( 1-tan(k*h*cos(th)/2)/tan(k*h/2) )
/ (sin(k*h*sin(th)/2)*sin(k*h*sin(th)/2));
// left
if ( i==0 ) {
psi_next[idx(0,j)] = - psi_previous[idx(1,j)]
+ (u1-1)/(u1+1)*( psi_next[idx(1,j)]+psi_previous[idx(0,j)] )
+ 2/(u1+1)*( psi_current[idx(1,j)] + psi_current[idx(0,j)] )
+ 0.5*u2*u2/(u1+1)*( psi_current[idx(1,j+1)]
+ psi_current[idx(1,j-1)] - 2*psi_current[idx(1,j)]
+ psi_current[idx(0,j+1)] + psi_current[idx(0,j-1)]
- 2*psi_current[idx(0,j)] );
}
// right
if ( i==Nx-1 ) {
psi_next[idx(Nx-1,j)] = - psi_previous[idx(Nx-2,j)]
+ (u1-1)/(u1+1)*( psi_next[idx(Nx-2,j)]+psi_previous[idx(Nx-1,j)] )
+ 2/(u1+1)*( psi_current[idx(Nx-2,j)] + psi_current[idx(Nx-1,j)] )
+ 0.5*u2*u2/(u1+1)*( psi_current[idx(Nx-2,j+1)]
+ psi_current[idx(Nx-2,j-1)] - 2*psi_current[idx(Nx-2,j)]
+ psi_current[idx(Nx-1,j+1)] + psi_current[idx(Nx-1,j-1)]
- 2*psi_current[idx(Nx-1,j)] );
}
// bottom
if ( j==0 ) {
psi_next[idx(i,0)] = - psi_previous[idx(i,1)]
+ (u1-1)/(u1+1)*( psi_next[idx(i,1)]+psi_previous[idx(i,0)] )
+ 2/(u1+1)*( psi_current[idx(i,1)] + psi_current[idx(i,0)] )
+ 0.5*u2*u2/(u1+1)*( psi_current[idx(i+1,1)]
+ psi_current[idx(i-1,1)] - 2*psi_current[idx(i,1)]
+ psi_current[idx(i+1,0)] + psi_current[idx(i-1,0)]
- 2*psi_current[idx(i,0)] );
}
// top
if ( j==Ny-1 ) {
psi_next[idx(i,Ny-1)] = - psi_previous[idx(i,Ny-2)]
+ (u1-1)/(u1+1)*( psi_next[idx(i,Ny-2)]+psi_previous[idx(i,Ny-1)] )
+ 2/(u1+1)*( psi_current[idx(i,Ny-2)] + psi_current[idx(i,Ny-1)] )
+ 0.5*u2*u2/(u1+1)*( psi_current[idx(i+1,Ny-2)]
+ psi_current[idx(i-1,Ny-2)] - 2*psi_current[idx(i,Ny-2)]
+ psi_current[idx(i+1,Ny-1)] + psi_current[idx(i-1,Ny-1)]
- 2*psi_current[idx(i,Ny-1)] );
}
}
// Update field
void Update( void )
{
// Shift memory target
double* temp = psi_previous;
psi_previous = psi_current;
psi_current = psi_next;
psi_next = temp;
// Update field
for ( int i=1; i<Nx-1; i++ ) {
for ( int j=1; j<Ny-1; j++ ) {
// Get index
int id = idx( i, j );
// additional difference
double dx2dy2 =
+ psi_current[idx(i-1,j+1)] - 2*psi_current[idx(i ,j+1)]
+ psi_current[idx(i+1,j+1)] - 2*psi_current[idx(i-1,j )]
+ 4*psi_current[idx(i ,j )] - 2*psi_current[idx(i+1,j )]
+ psi_current[idx(i-1,j-1)] - 2*psi_current[idx(i ,j-1)]
+ psi_current[idx(i+1,j-1)];
// NS-FDTD
psi_next[id] = - psi_previous[id] + 2*psi_current[id]
+ u[id]*u[id]*( psi_current[idx(i+1,j)]
+ psi_current[idx(i,j+1)] + psi_current[idx(i-1,j)]
+ psi_current[idx(i,j-1)] - 4*psi_current[id]
+gamma1[id]*dx2dy2 );
// Add incident field
psi_next[id] += ( 1/(n[id]*n[id]) - 1 )
* ( Source(k,i,omega,t+dt)
- 2*Source(k,i,omega,t) + Source(k,i,omega,t-dt) );
}
}
// Set boundary condition
for ( int j=1; j<Ny-1; j++ ) {
nsMurABC(0,j);
nsMurABC(Nx-1,j);
}
for ( int i=1; i<Nx-1; i++ ) {
nsMurABC(i,0);
nsMurABC(i,Ny-1);
}
// Update t
t += dt;
}
// Incident field
double Source( double k, double x, double omega, double t )
{
// damping coefficient
double w = 1.0 - exp(-pow(0.01*t,2));
return w * sin( k*x - omega*t );
}
// Get number of grid points
int GetNx()
{
return Nx;
}
int GetNy()
{
return Ny;
}
// Get current field value
double GetValue( int i, int j )
{
return psi_current[idx(i,j)];
}
// Get intensity
double GetIntensity( int i, int j )
{
// Get index
int id = idx( i, j );
// Get field values
double v0 = psi_next[id];
double v1 = psi_current[id];
double v2 = psi_previous[id];
// Calculate time difference
double a = ( v0-v2 ) / ( 2*sin(omega*dt) );
double b = ( v0+v2-2.0*v1 ) / ( 4.0*sin(omega*dt/2)*sin(omega*dt/2) );
// Return intensity
return a*a + b*b;
}
};
|
The functions are
- Initialize:
(1) Define simulation parameters; (2) Allocate field and coefficient memoris; (3) Initialize field and set coefficients.
- Finalize:
Release memories.
- idx:
Map 2D index on 1D one.
- IsInCircle:
Determine inside or outsider cylinder.
- FuzzyModel:
Set refractive index based on the fuzzy model.
- SetCoefficients:
Set NS-FDTD coefficients.
- nsMurABC:
Set the nonstandard 2nd-order Mur ABC at (1) left, (2) right, (3) bottom, and (4) top boundaries.
- Update:
Calculate next time step. (1) Shift memory target; (2) Update field using the NS-FDTD algorithm. (3) Set nonstandard Mur ABC; (4) Update time step.
- GetNumNx, GetNumNy:
Return the number of grid points.
- GetValue:
Return calculated field value indexed by id.
- GetIntensity:
Return intensity indexed by id.
OpenGL Visualization
Let us program an interactive calculation using the GLUT.
Source 2 is a main program includes GLUT visualization.
Source. 2. GLUT visualization of FDTD simulation. [Download Source 2]
// Include header files
#include "fdtd2d.h"
#include "glut.h"
// FDTD2D class
FDTD2D fdtd;
// Keyboard event
void keyboard( unsigned char key, int x, int y )
{
switch ( key ) {
// pushed 't' key
case 't':
fdtd.Update(); // Update field
glutPostRedisplay(); // Redisplay
break;
default:
break;
}
}
// Transform from value to color
void Val2Col( double v, double* r, double* g, double* b )
{
// Normalize value
float nv = max( 0.0, min( 1.0, abs(v) ) );
// Get color
if ( v >= 0.75 ) { *r = 1.0; *g = 4.0*(1.0-nv); *b = 0.0; }
else if ( v >= 0.50 ) { *r = 4.0*(nv-0.5); *g = 1.0; *b = 0.0; }
else if ( v >= 0.25 ) { *r = 0.0; *g = 1.0; *b = 4.0*(0.5-nv); }
else { *r = 0.0; *g = 4.0*nv; *b = 1.0; }
}
// Redisplay event
void display( void )
{
// Clear background
glClear( GL_COLOR_BUFFER_BIT );
// Begin to draw points
glBegin( GL_POINTS );
// Draw distribution
double r, g, b;
for ( int i=0; i<fdtd.GetNx(); i++ ) {
for ( int j=0; j<fdtd.GetNy(); j++ ) {
// Get intensity
double intensity = fdtd.GetIntensity( i, j );
// point coordinates
double x = -1.0 + 2*(i)/(double)(fdtd.GetNx()-1);
double y = -1.0 + 2*(j)/(double)(fdtd.GetNy()-1);
// Coloring
Val2Col( intensity, &r, &g, &b );
glColor4d( r, g, b, 1 );
// Draw point
glVertex2d( x, y );
}
}
// End to draw lines
glEnd();
// Update view
glFlush();
}
// Main function
int main( int argc, char** argv )
{
// Initialize
fdtd.Initialize();
// Initialize GL
glutInitWindowPosition( 50, 50 ); // window position
glutInitWindowSize( 400, 400 ); // window size
glutInitDisplayMode( GLUT_SINGLE ); // display mode
glutInit( &argc, argv ); // Initialize GLUT
glutCreateWindow( "FDTD" ); // Create window
glutKeyboardFunc( keyboard ); // Register keyboard events
glutDisplayFunc( display ); // Register display events
glPointSize( 8 ); // point size
// GL loop
glutMainLoop();
// Finalize
fdtd.Finalize();
return 0;
}
|
Here we show rough flow of functions,
- keyboard:
Reply to keyboard events, where for t-key: (1) Update wave field; (2) Post a display event.
- Val2Col:
Intensity coloring (blue < green < red).
- display:
Draw figures: (1) Clear canvas; (2) Draw colored intensity distribution; (3) Display the figure.
- main:
(1) Initialize FDTD class; (2) Initialize OpenGL using GLUT library; (3) Start main loop. This loop is held up processing events until the window is closed; (4) Finalize FDTD class.
Figures 3 show the FDTD simulation results. Figure (a), (b), (c) are analytic, S-FDTD, NS-FDTD results, respectively.
The NS-FDTD algorithm provides remarkably higher accuracy than the FDTD algorithm.
.jpg) |
.gif) |
.gif) |
| (a) Analytic |
(b) Standard FDTD |
(c) Nonstandard FDTD |
Fig. 3. Intensity distributions of Mie scattering simulation: (a) Analytic; (b) Standard FDTD; and (c) Nonstandard FDTD.
Bibliography:
[1] P. W. Barber, S. C. Hill, "Light Scattering by Particles: Computational Methods," World Scientific (1989).
Copyright (C) 2011 Naoki Okada, All Rights Reserved.
|
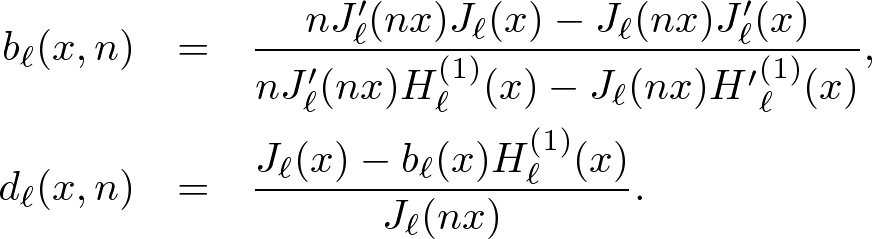 . . . (6)
. . . (6)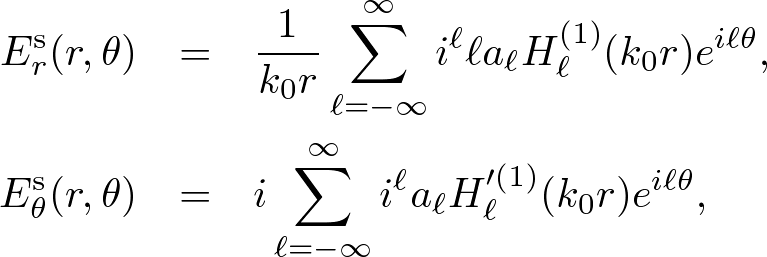 . . . (7)
. . . (7)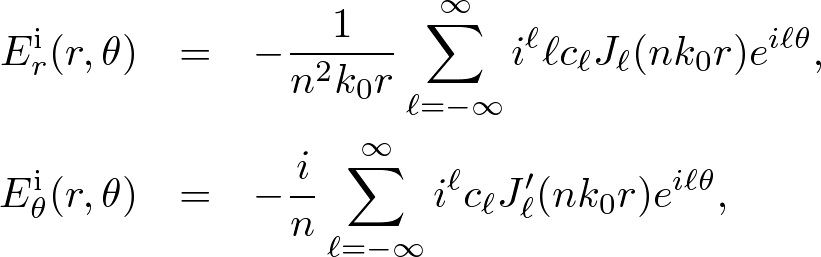 . . . (8)
. . . (8)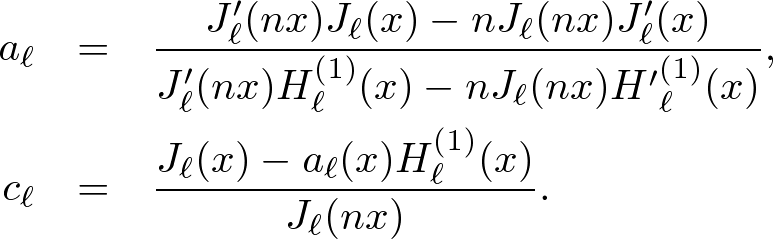 . . . (9)
. . . (9)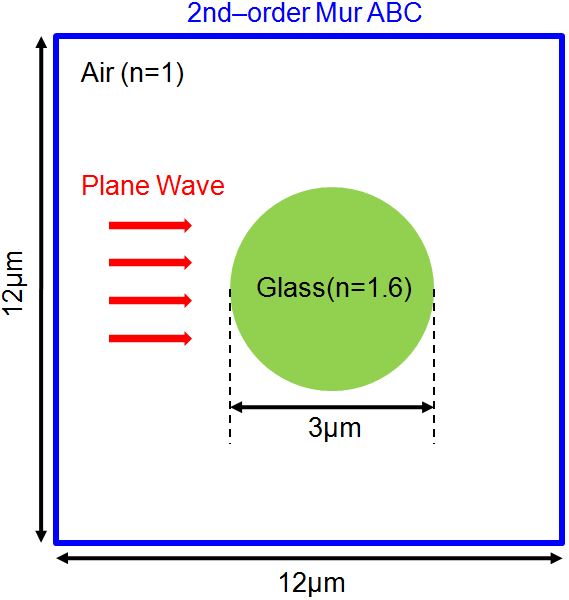
.jpg)
.gif)
.gif)