Nonstandard FDTD Theory

Beginner Course

1. Finite Difference Model
2. 1D Wave Equation
3. 1D Stability
4. 1D Boundary Condition
5. Dimensionless Form
6. 1D Example

Intermediate Course

1. 2D Wave Equation
2. 2D Maxwell's Equations
3. Scattered Field
4. 2D Stability
5. 2D Boundary Condition
6. Scatterer Representation
7. Intensity
8. 2D Example

Advanced Course

1. 3D Wave Equation
2. 3D Maxwell's Equations
3. 3D Stability
4. Conductive Media
5. Perfectly Matched Layer

2. 1D Wave Equation

The one-dimensional (1D) wave equation governs basic wave propagation. The wave equation is easily discretized by using the central finite difference model. We can numerically solve the discrete wave equation and understand wave phenomena.

Standard FDTD Algorithm

The one-dimensional wave equation is defined by

where ∂_t=∂/∂t, (∂_x is analogously defined to ∂_t), and v is the wave speed. Discretizing x = iΔx, t = nΔt (i, n = integer), we simply write

Using the central finite difference model, we find

where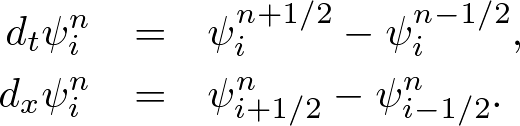

Expanding the temporal difference, d_t²ψ_iⁿ, we obtain a "1D standard finite difference time domain (FDTD) algorithm,"

where

Nonstandard FDTD Algorithm

The central finite difference model is given by

whereas we introduce an exact expression,

where s(Δx) is a correction function. Here we suppose a monochromatic wave,

where k = wavenumber and ω = angular frequency. Note that any electromagnetic wave is a superposition of monochromatic waves, we find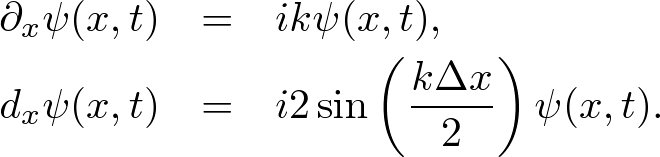

Putting s(Δx) into s(k, Δx), we obtain

Although this approach is not always valid because the following definition must be satisfied,

(12) is fortunately satisfied. Thus, (8) is an exact central finite difference model what called nonstandard finite difference model" [1, 2].

Similarly for the temporal derivative, we find

Expanding the temporal difference, d_t²ψ_iⁿ, we obtain a "1D nonstandard FDTD algorithm,"

where

where we used v = ω / k.

Bibliography:
[1] R. E. Mickens, "Nonstandard Finite Difference Models of Differential Equation," World Scientific (1994).
[2] J. B. Cole, "A high accuracy fdtd algorithm to solve microwave propagation and scattering problems on a coarse grid," IEEE Trans. Microwave Theory and Tech, 43, 9, pp. 2053-2058 (1995).

Copyright (C) 2011 Naoki Okada, All Rights Reserved.