Nonstandard FDTD Theory

Beginner Course

1. Finite Difference Model
2. 1D Wave Equation
3. 1D Stability
4. 1D Boundary Condition
5. Dimensionless Form
6. 1D Example

Intermediate Course

1. 2D Wave Equation
2. 2D Maxwell's Equations
3. Scattered Field
4. 2D Stability
5. 2D Boundary Condition
6. Scatterer Representation
7. Intensity
8. 2D Example

Advanced Course

1. 3D Wave Equation
2. 3D Maxwell's Equations
3. 3D Stability
4. Conductive Media
5. Perfectly Matched Layer

Welcome to Beginner Course!

This course mainly introduces one-dimensional standard and nonstandard FDTD theories. The computer simulation additionally requires a numerical stability and a boundary condition. In the beginner course, we illustrate these basic theories and simulatin techniques, and demonstrate example FDTD calculation with program codes.

1. Finite Difference Model

Many complex differential equations have no analytical solutions. The numerical simulation is a unique approach to solve such equations. Here we introduce basic finite difference models:

• Forward Finite Difference Model
• Backward Finite Difference Model
• Central Finite Difference Model
• Higher-Order Finite Difference Model

Forward Finite Difference Model

The forward perturbation of an one-dimensional function is given by Taylor series,

If Δx is sufficiently small, the first order derivative is approximated by

(2) is called a first-order "forward finite difference model."

Backward Finite Difference Model

Similarly, the backward perturbation is expanded to

The first-order "backward finite difference model" is defined by

Central Finite Difference Model

The forward and backward finite difference models are first-order approximations. On the other hand, subtracting (3) from (1), we find

where the term of the order of Δx² is canceled out. Replacing Δx with Δx/2, we find

(6) is called a second-order "central finite difference model." In addition, d²f(x)/dx² is approximated by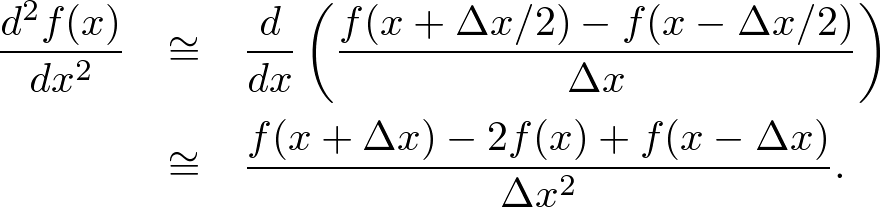

Higher-Order Finite Difference Model

More accurate finite difference approximations can be found. For example, d²f(x)/dx² is approximated by the fourth-order finite difference model,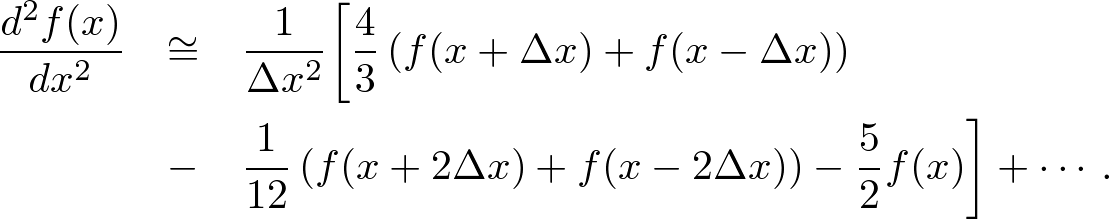

However, replacing the second-order differential equation with the fourth-order finite difference model yields four solutions, although the differential equation analytically has only two solutions. The unexpected solutions in the difference equation may cause numerical instability. Based on analytical and numerical studies for a large number of ordinary and partial differential equations, Ronald E. Mickens concludes that (quotation from [1])

• The orders of the discrete derivatives must be exactly equal to the orders of the corresponding derivatives of the differential equations.
• Special solutions of the differential equations should also be special (discrete) solutions of the finite-difference models.
• The finite-difference equations should not have solutions that do not correspond exactly to solutions of the differential equations.

Thus, for the second-order differential equation such as the wave equation, the second-order central finite difference model is better than higher-order ones.

Bibliography:
[1] R. E. Mickens, "Nonstandard Finite Difference Models of Differential Equation," World Scientific (1994).

Copyright (C) 2011 Naoki Okada, All Rights Reserved.