Welcome to Nonstandard FDTD TheoryIn this website you can find the nonstandard finite difference time domain (FDTD) theory and example simulations. We provide three courses, Beginner, Intermediate, and Advanced. The biginner course mainly introduces the one-dimensional standard and nonstandard FDTD theories. The intermediate course introduce two-dimensional FDTD theories. The two-dimensional NS-FDTD theory holds a key (combinations of finite difference models) to high accuracy in Maxwell's equations. The advanced course introduce three-dimensional FDTD theories and apply it to conductive media. Learing Course
Advantage of Nonstandard FDTD Algorithm
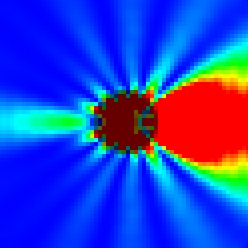
The FDTD algorithm is one of the most famous algorithms to calculate electromagnetic wave propagation. The FDTD algorithm can calculate arbitrary shapes, nonlinear media, and wideband waves. However, complicated nanostructures, such as photonic crystals, metamaterials, and Morpho butterfly scales, cannot be accurately calculate by the FDTD algorithm because computational resources are limited. Whereas, the nonstandard FDTD algorithm is much more accurate than the conventional FDTD algorithm by optimizing to monocromatic wave propagation. Higher accuracy also means that the computational cost is reduced to obtain accuracy equivalent to the conventional FDTD calculation. Using the nonstandard FDTD algorithm, we has successfully to accurately simulate whispering gallery modes which cannot be well-calculated by the conventional FDTD algorithm. Above figures show an example simulation of the Mie scattering. Figure (a) is the analytic solution by Mie theory. Figures (b) and (c) are simulation results on a course grid using conventional and nonstandard FDTD algorithms, respectively. The nonstandard FDTD result gives close agreement with Mie theory and is much more accurate than the conventional FDTD one.
Copyright (C) 2011 Naoki Okada, All Rights Reserved.
|