Nonstandard FDTD Theory

Beginner Course

1. Finite Difference Model
2. 1D Wave Equation
3. 1D Stability
4. 1D Boundary Condition
5. Dimensionless Form
6. 1D Example

Intermediate Course

1. 2D Wave Equation
2. 2D Maxwell's Equations
3. Scattered Field
4. 2D Stability
5. 2D Boundary Condition
6. Scatterer Representation
7. Intensity
8. 2D Example

Advanced Course

1. 3D Wave Equation
2. 3D Maxwell's Equations
3. 3D Stability
4. Conductive Media
5. Perfectly Matched Layer

Welcome to Advanced Course!

This course expands the nonstandard FDTD algorithm to three dimensions and conductive media. The perfectly matched layer consists of pseudo conductive media and is the most effective absorbing boundary condition. In the advanced course, we illustrate these higher theories.

1. 3D Wave Equation

The three-dimensional (3D) wave equation is given by

where ∇ = (∂_x, ∂_y, ∂_z). Let us find a S- and NS-FDTD algorithms for this wave equation.

Standard FDTD Algorithm

Let x = ih, y = jh, z = kh (h = Δx = Δy = Δz), t = Δt, and we simply write ψ(x, y, z, t) = ψ_i,j,kⁿ. Using the central finite difference model, we obtain

where d_S = (d_x, d_y, d_z) and d_S² = d_x² + d_y² + d_z². Expanding the temoporal difference operator, we obtain a "3D S-FDTD algorithm,"

where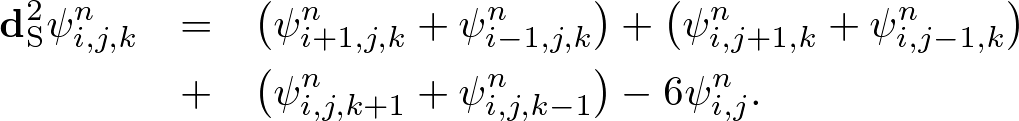

For a monochromatic wave, ψ(x,y,z,t) = e^{i(k_xx+k_yy+k_zz±ωt)} where (k_x,k_y,k_z) = k(cosθsinφ, sinθsinφ, cosφ), the spatial difference error of d_S²/h² becomes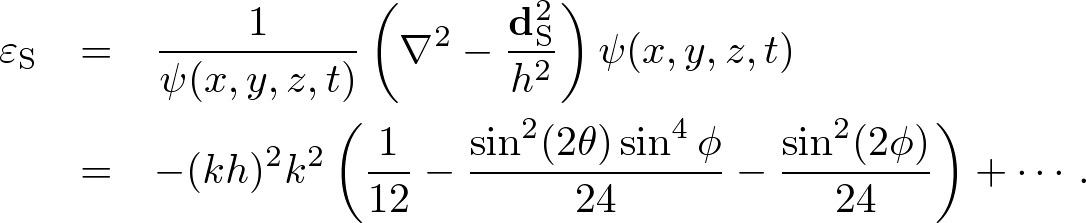

Nonstandard FDTD Algorithm

For the monochromatic wave, ψ(x,y,z,t) = e^{i(k_xx+k_yy+k_zz±ωt)}, the temporal derivative is exactly discretized by

As discussed in the 2D NS-FDTD algorithm, the spatial difference operator must be angularly independent. Combining difference operators, we define

where γ₁ is given in two dimensions due to corresponding for d_zψ(x,y,z,t) = 0, and γ₂ satisfies

where s(k,h) = (2/k)sin(kh/2). Solving (8), we obtain

The spatial difference error of d_NS²/s(k,h)² becomes

Using (6) and (8), we obtain a "3D NS-FDTD algorithm,"

Copyright (C) 2011 Naoki Okada, All Rights Reserved.