Beginner Course
Intermediate Course
Advanced Course4. Conductive MediaThe conductive Maxwell's equations are defined by where σ, σ* are the electric and magnetic conductivities, respectively. In conductive media, electromagnetic waves are exponentially decayed. Here we apply the standard and nonstandard FDTD algorithms and stabilities to conductive media. Standard FDTD Algorithm for the Absorbing Wave EquationApplying ∇× to both sides of (1) and using the vector identity, ∇×∇×E = ∇(∇⋅E) - ∇2E, we obtain an absorbing wave equation in homogeneous media, where The solution of the absorbing wave equation is where Using the S-FDTD algorithm, we obtain where α = aΔt, α* = a*Δt, and Let x = ih, y = jh, z = kh, t = nΔt (i,j,k,n are integers). Expanding the temoporal difference operators, we obtain a "S-FDTD algorithm for the absorbing wave equation," 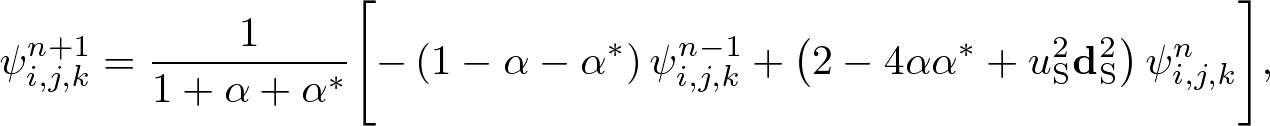 . . . (8) . . . (8)where we write ψi,j,kn = ψ(ih,jh,kh,nΔt). Nonstandard FDTD Algorithm for the Absorbing Wave EquationThe NS-FDTD algorithm is derived by optimizing to the monochromatic wave (4). For the spatial derivative, we already have a high accuracy difference operator, Vanishing temporal difference errors, we require that we choose coefficients as (10) is exactly satisfied. The temporal-spatial difference operators give 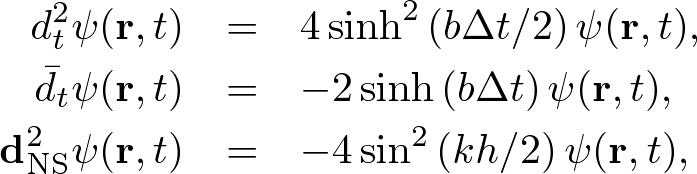 . . . (11) . . . (11)where Substituting (11) into (10) and requiring that the imaginary part vanishes, we find 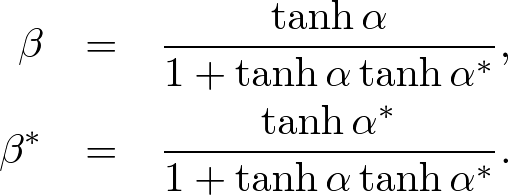 . . . (13) . . . (13)Setting the real part to zero, we obtain Expanding the temporal difference operators, we obtain a "NS-FDTD algorithm for the absorbing wave equation," Standard Yee Algorithm for Conductive Maxwell's EquationsUsing the S-FDTD algorithm in the same way as the 3D Yee cell, the conductive Maxwell's equations are discretized by 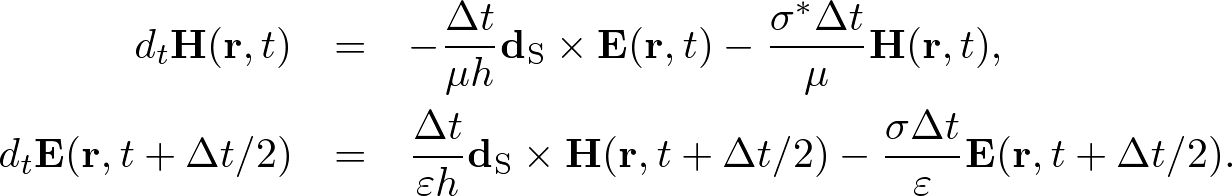 . . . (16) . . . (16)Since H(r, t) and E(r, t+Δt) are not matched to the temporal arrangement in the Yee cell, we approximate 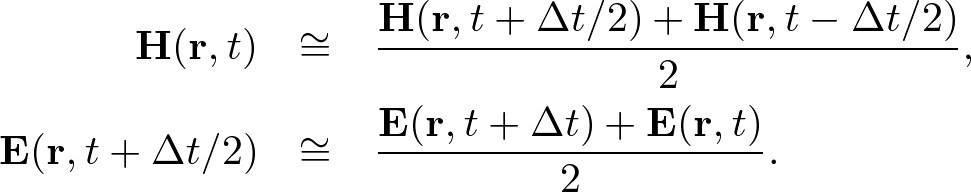 . . . (17) . . . (17)Expanding the temporal differences, we obtain a "S-Yee algorithm for conductive Maxwell's equations," 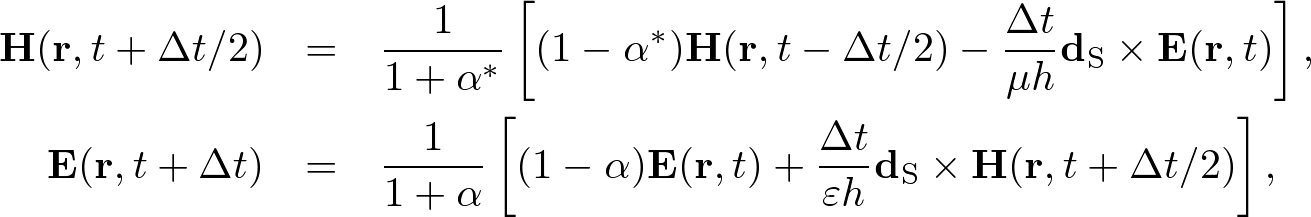 . . . (18) . . . (18)where α = σΔt/(2ε) and α* = σ*Δt/(2μ). Nonstandard Yee Algorithm for Conductive Maxwell's EquationsBased on the non-conductive NS-FDTD algorithm, we define 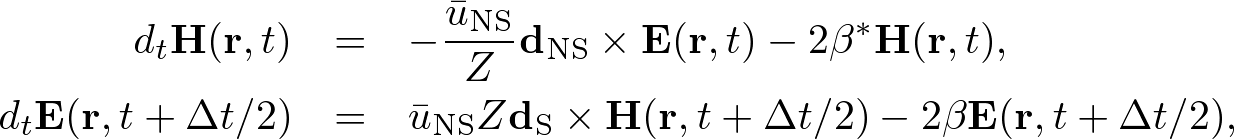 . . . (19) . . . (19)where Z = (μ/ε)1/2. (19) is a high accracy form optimized to monochromatic wave propagation, because it is equivalent to the NS-FDTD algorithm for the absorbing wave equation (15). Expanding the temporal differences and using (13), we obtain a "NS-Yee algorithm for conductive Maxwell's equations," 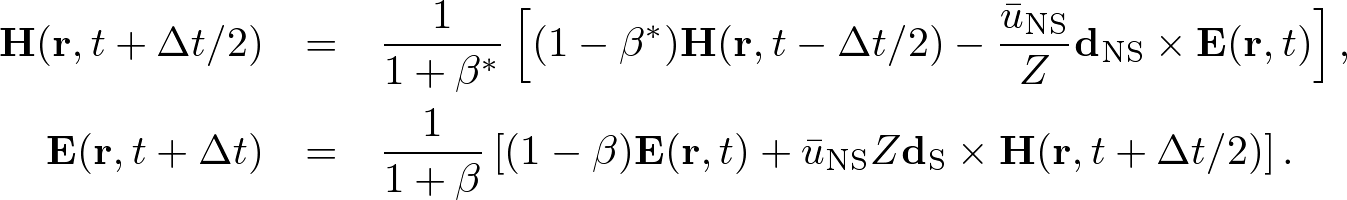 . . . (20) . . . (20)Numerical StabilityThe S- and NS-FDTD algorithms for the absorbing wave equation are rewritten in the form, 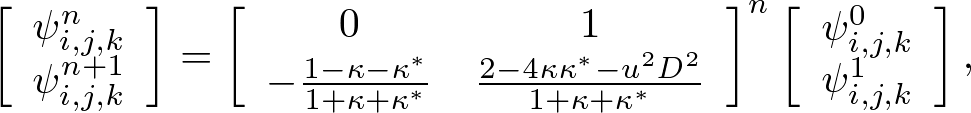 . . . (21) . . . (21)where Since the eigenvalue of the matrix gives the stability we find 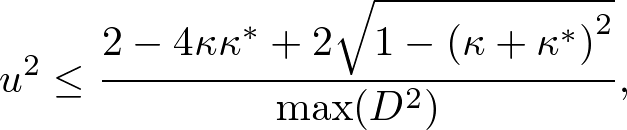 . . . (23) . . . (23)where max(D2) is similarly defined as non-conductive media.
Copyright (C) 2011 Naoki Okada, All Rights Reserved.
|