Nonstandard FDTD Theory

Beginner Course

1. Finite Difference Model
2. 1D Wave Equation
3. 1D Stability
4. 1D Boundary Condition
5. Dimensionless Form
6. 1D Example

Intermediate Course

1. 2D Wave Equation
2. 2D Maxwell's Equations
3. Scattered Field
4. 2D Stability
5. 2D Boundary Condition
6. Scatterer Representation
7. Intensity
8. 2D Example

Advanced Course

1. 3D Wave Equation
2. 3D Maxwell's Equations
3. 3D Stability
4. Conductive Media
5. Perfectly Matched Layer

3. 3D Stability

The numerical stability for the wave equation is given by

where D is defined below.

S-FDTD Stability

For a monochromatic wave, ψ(x,y,z,t) = e^{i(k_xx+k_yy+k_zz±ωt)}, we obtain

where D is defined by d_S² ψ(x,y,z,t) = -D²ψ(x,y,z,t). To find max(D²), we solve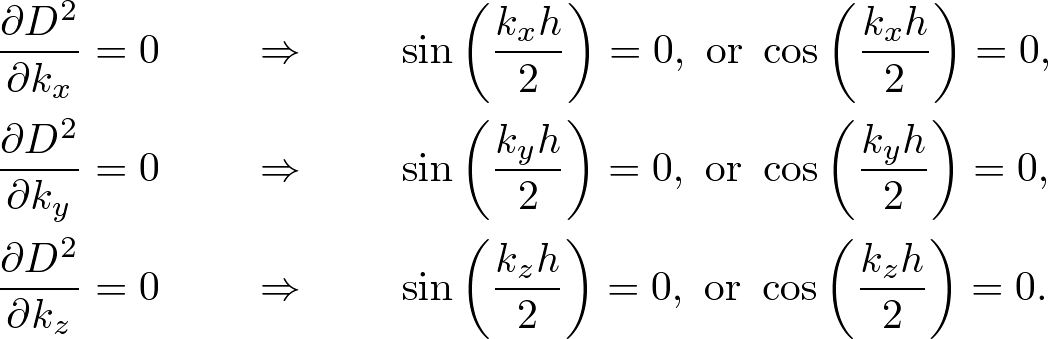

For cos(k_xh/2) = cos(k_yh/2) = cos(k_zh/2), max(D²) is given by

Since the stability of the S-FDTD algorithm is given by u_S² ≤ 4/max(D²), we obtain

where we use h = Δt = 1.

NS-FDTD Stability

In the 3D NS-FDTD algorithm D² is defined by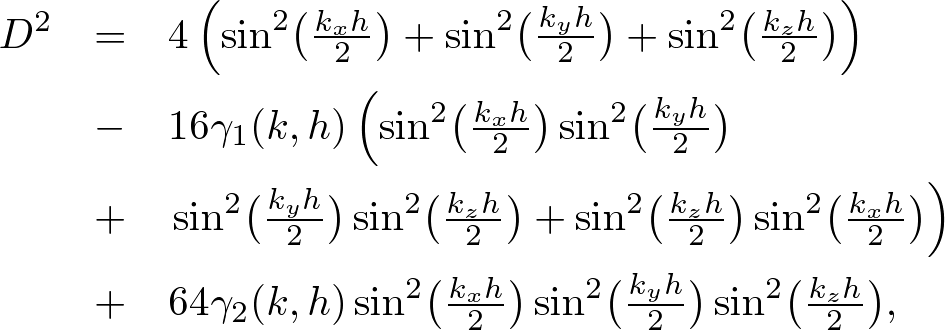

where D is defined by d_NS² ψ(x,y,z,t) = -D²ψ(x,y,z,t). To obtain max(D²), we solve

and we find

Substituting (8) into (6), we obtain

Since the stability of the NS-FDTD algorithm is given by u_NS² ≤ 4/max(D²), we obtain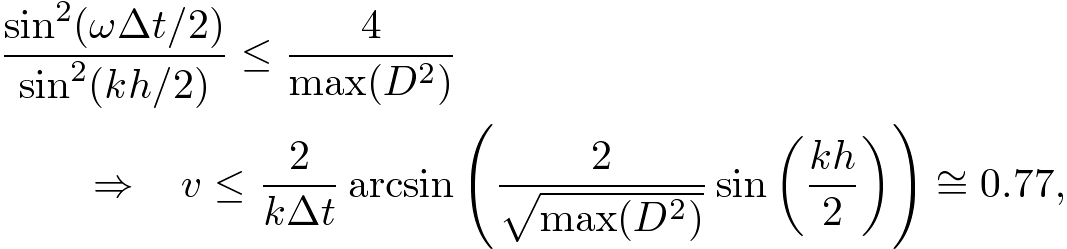

where we use k ∼ 0 and h = Δt = 1. In three dimensions, comparing with the S-FDTD stability, the value of v can be increased by about 35%.

Copyright (C) 2011 Naoki Okada, All Rights Reserved.