Nonstandard FDTD Theory

Beginner Course

1. Finite Difference Model
2. 1D Wave Equation
3. 1D Stability
4. 1D Boundary Condition
5. Dimensionless Form
6. 1D Example

Intermediate Course

1. 2D Wave Equation
2. 2D Maxwell's Equations
3. Scattered Field
4. 2D Stability
5. 2D Boundary Condition
6. Scatterer Representation
7. Intensity
8. 2D Example

Advanced Course

1. 3D Wave Equation
2. 3D Maxwell's Equations
3. 3D Stability
4. Conductive Media
5. Perfectly Matched Layer

5. 2D Boundary Condition

The two-dimensional perfect conductor and periodic boundary conditions are similar to one-dimensional ones. But the Mur absorbing boundary condition (ABC) is more complicated because the first-order Mur ABC is only valid for normal incidence. We derive the second-order Mur ABC which absorbs waves with wide angle.

2nd-order Standard Mur ABC

The 2D wave equation is given by

We obtain

Substituting a monochromatic wave, ψ(x,y,t) = e^{i(k_xx+k_yy±ωt)}, into (2), we obtain

Supposing k_y ≪ k, (3) becomes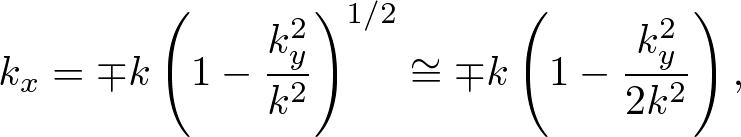

where we used the general binominal theorem,

Using ω ∼ ±i∂_t, k_x ∼ i∂_x, k_y ∼ i∂_y, we obtain second-order one-way wave equations,

Let us find the ABC at x = 0. Using the S-FDTD algorithm, we discretize (6) at t = nΔt, x = h/2, y = jh, and we obtain a "second-order standard (S) Mur ABC,"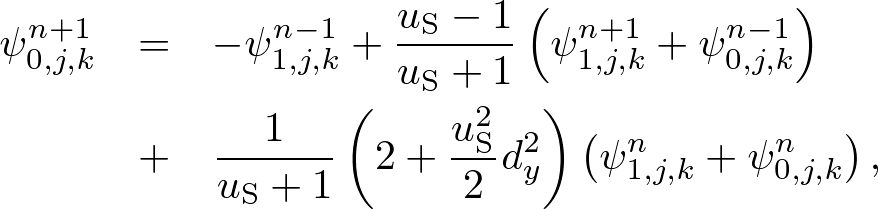

2nd-order Nonstandard Mur ABC

The second-order Mur ABC can be optimized to monochromatic wave propagation, but it depends on wave direction. The 2D angular optimization is introduced in [1]. Let (k_x, k_y) = k(cosθ, sinθ), we obtain a "second-order nonstandard (NS) Mur ABC,"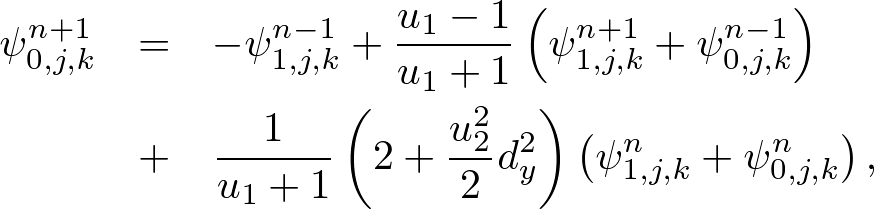

where u₁ = tan(ωΔt/2)/tan(kh/2) and

Empirically, θ = π/3 gives a good absorption.

Bibliography:
[1] J. B. Cole, D. Zhu, "Improved version of the second-order mur absorbing boundary condition based on a nonstandard finite difference model," Applied Computational Electromagnetics Society (ACES), 24, 4 (2009).

Copyright (C) 2011 Naoki Okada, All Rights Reserved.