Nonstandard FDTD Theory

Beginner Course

1. Finite Difference Model
2. 1D Wave Equation
3. 1D Stability
4. 1D Boundary Condition
5. Dimensionless Form
6. 1D Example

Intermediate Course

1. 2D Wave Equation
2. 2D Maxwell's Equations
3. Scattered Field
4. 2D Stability
5. 2D Boundary Condition
6. Scatterer Representation
7. Intensity
8. 2D Example

Advanced Course

1. 3D Wave Equation
2. 3D Maxwell's Equations
3. 3D Stability
4. Conductive Media
5. Perfectly Matched Layer

Welcome to Intermediate Course!

This course mainly introduces two-dimensional standard and nonstandard FDTD theories. The two-dimensional FDTD theory is very important, because it includes polarized Maxwell's equations and various high-accuracy calculation techniques such as scatterer representations on a numerical grid and a difference combination of nonstandard FDTD theory. In the intermediate, we illustrate these crucially important theories and techniques, and demonstrate example Mie scattering with program codes.

1. 2D Wave Equation

The two-dimensional (2D) wave equation corresponds to a polarization in Maxwell's equations. The nonstandard FDTD algorithm for the 2D wave equation holds a fundamental key (which combination of finite difference models) to high accuracy electromagnetic computation.

Standard FDTD Algorithm

The two-dimensional wave equation is defined by

where ∇ = (∂_x, ∂_y). Let x = ih, y = jh (h = Δx = Δy), t = Δt, and we simply write

Using the central finite difference model, we obtain

where d_S = (d_x, d_y) and d_S² = d_x² + d_y². Expanding the temporal difference operator, we obtain a "2D S-FDTD algorithm."

where

For a monochromatic wave ψ(x,y,t) = e^{i(k⋅r±ωt)} where k = (k_x, k_y) = k(cosθ,sinθ) and r = (x, y), the spatial difference error of d_S²/h² becomes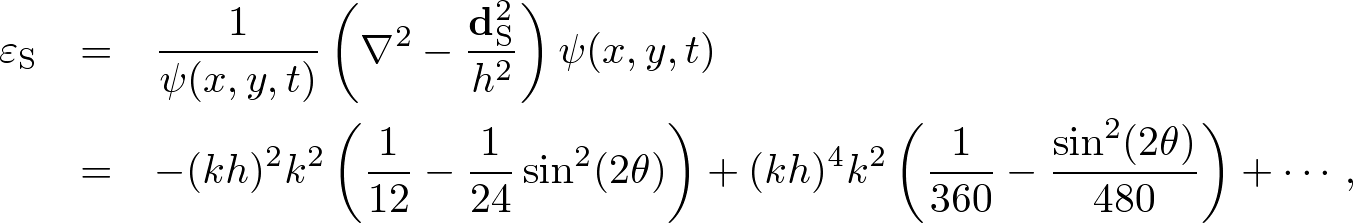

note that ε_S ∝ (h/λ)² due to k = 2π/λ.

Nonstandard FDTD Algorithm

In the similar way to the 1D NS-FDTD algorithm, we try to optimize to amonochromatic wave, ψ(x,y,t) = e^{i(k⋅r±ωt)}. For the temporal derivative, we can find the exact expression,

Whereas for the spatial derivative, we obtain

(8) is an exact expression, but s(k,h) depends on θ. In two dimensions it is impossible to know θ at all grid points, because scattered waves propagate in any direction. For simplicity, let θ = mπ/2 (m = integer). We obtain an exact expression,

The spatial difference error of d_S²/s(k,h)² becomes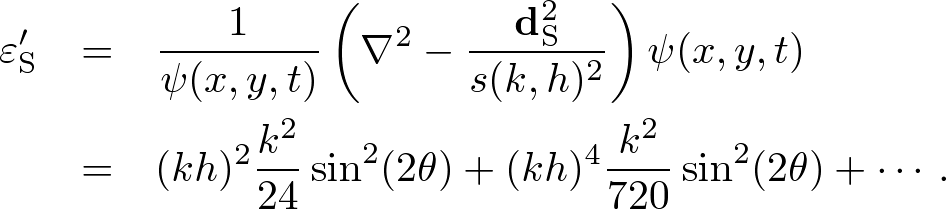

The angular dependence is canceled out by combining d_S² with another difference model d_x²d_y² refers cross grid points [1]. We define

where γ₁(k,h) is found by solving

We find

The spatial difference error of d_NS²/s(k,h)² becomes

note that ε_NS ∝ (h/λ)⁶ and ε_NS ≪ ε_S. Using (7) and (12), we obtain a "2D NS-FDTD algorithm,"

Bibliography:
[1] J. B. Cole, "High-accuracy yee algorithm based on nonstandard finite differences: New developments and verifications," IEEE Trans. Antennas and Propag., 50, 9, pp. 1185-1191 (2002).

Copyright (C) 2011 Naoki Okada, All Rights Reserved.