Nonstandard FDTD Theory

Beginner Course

1. Finite Difference Model
2. 1D Wave Equation
3. 1D Stability
4. 1D Boundary Condition
5. Dimensionless Form
6. 1D Example

Intermediate Course

1. 2D Wave Equation
2. 2D Maxwell's Equations
3. Scattered Field
4. 2D Stability
5. 2D Boundary Condition
6. Scatterer Representation
7. Intensity
8. 2D Example

Advanced Course

1. 3D Wave Equation
2. 3D Maxwell's Equations
3. 3D Stability
4. Conductive Media
5. Perfectly Matched Layer

2. 2D Maxwell's Equations

The non-conductive and non-dispersive Maxwell's equations are given by

where H = (H_x, H_y, H_z) is the magnetic field, E = (E_x, E_y, E_z) is the electric field, μ is the permeability, and ε is the permittivity. In two-dimensions the Maxwell's equations are separated into two-independent modes: transverse magnetic (TM) and transverse electric (TE) modes. In the TM mode (E parallel to media interfaces), the Maxwell's equations become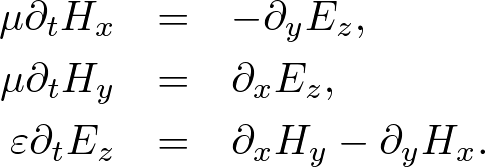

Whereas in the TE mode (E perpendicular to media interfaces), the Maxwell's equations become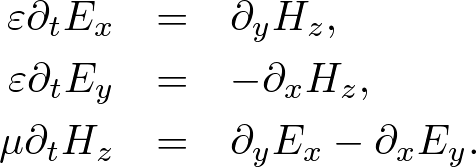

These Maxwell's equations can be solved by the FDTD algorithm what is called "Yee algorithm."

Standard Yee Algorithm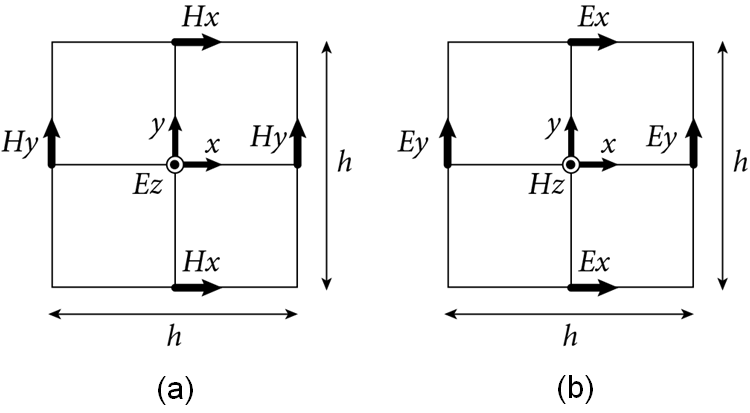

Fig. 1. Yee cell in two dimensions. h is the grid spacing. E_x, E_y, E_z are electric field components. H_x, H_y, H_z are magnetic field components. (a) E_z, H_x, H_y alternately lie on the grid in TM mode. (b) E_x, E_y, H_z alternately lie in TE mode.

In 1996, K. S. Yee developed a staggered grid what called "Yee cell." The Maxwell's equations are wisely discretized on the Yee cell using the central finite difference model. As shown in Fig. 1, we define the staggered grid,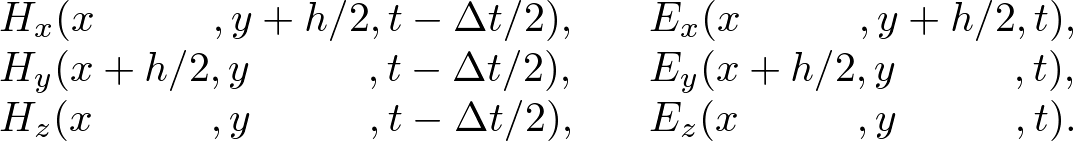

We can alternately update E and H. Using the S-FDTD algorithm on the Yee cell, the Maxwell's equations are discretized by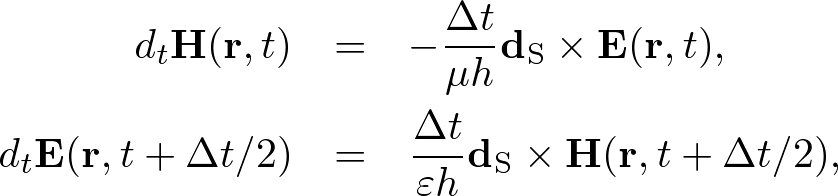

where d_S = (d_x, d_y, 0). Expanding the temporal difference operators, we obtain a "2D standard (S) Yee algorithm,"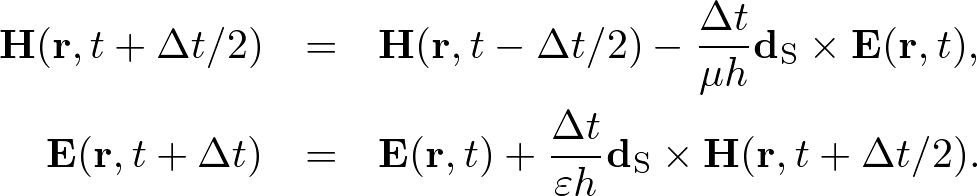

Nonstandard Yee Algorithm

The Maxwell's equations are transformed to the wave equation. Applying ∇× to both sides of (1), we obtain

In homogeneous media, Gauss' law gives, ∇⋅E = 0. Using a vector identity, we obtain

Substituting (7) and (8) into (1), we obtain the wave equation,

where v = 1/(με)^1/2. In inhomogeneous media, Gauss'law gives, ∇⋅(εE) = E⋅∇ε + ε∇⋅E = 0. In the TM mode, ∇⋅E = 0 because E⊥∇ε. In the TE mode, however, ∇⋅E ≠ 0 and the coupled wave equations are derived,

We already have the NS-FDTD algorithm for the homogeneous wave equation. If we find a difference operator, d_NS, satisfies d_NS² = d_NS⋅d_NS, a high-accuracy discretization for the Maxwell's equations is directly transformed from the NS-FDTD algorithm for the wave equation. But such difference operator does not exist because it is impossible to calculate d_NS = (d_S + γ₁d_x²d_y²)^1/2. Instead we require that

where

Using (12), the Maxwell's equations are discretized by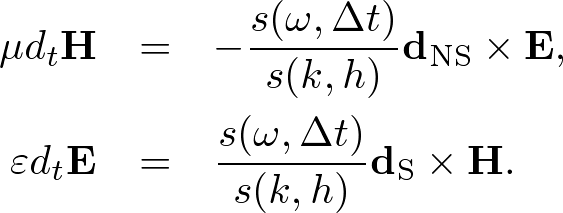

Applying d_S× to both sides of (13), we obtain

In homogeneous media, Gauss' law gives

Substituting (14) and (15) into (13), we obtain the NS-FDTD algorithm for the homogeneous wave equation,

Thus, (13) is a high accuracy form optimized to monochromatic wave propagation. Expanding d_tH and d_tE, we obtain a "2D nonstandard (NS) Yee algorithm,"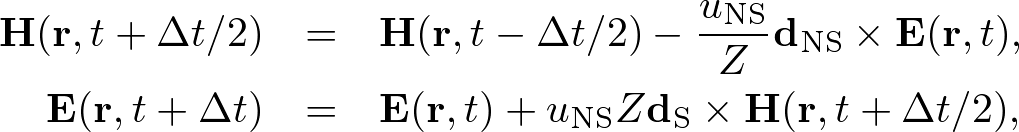

where Z = (μ/ε)^1/2 is the wave impedance. This transform is an approximation in the TE mode, nevertheless, the NS-Yee algorithm provides much higher accuracy than the S-Yee one. To reduce the numerical errors, we additionally can modify the form,

where

Copyright (C) 2011 Naoki Okada, All Rights Reserved.