Nonstandard FDTD Theory

Beginner Course

1. Finite Difference Model
2. 1D Wave Equation
3. 1D Stability
4. 1D Boundary Condition
5. Dimensionless Form
6. 1D Example

Intermediate Course

1. 2D Wave Equation
2. 2D Maxwell's Equations
3. Scattered Field
4. 2D Stability
5. 2D Boundary Condition
6. Scatterer Representation
7. Intensity
8. 2D Example

Advanced Course

1. 3D Wave Equation
2. 3D Maxwell's Equations
3. 3D Stability
4. Conductive Media
5. Perfectly Matched Layer

3. Scattered Field

The FDTD algorithm can separate incident and scattered fields and observe only latter. The scattered field formulation is effective because the total field is also included in the formulation and can be observed without transformation.

Scattered Field Form for Wave Equation

The wave equation is given by

where v₀ is the phase speed in vacuum and n is the refractive index. We separate

where ψ^s is the scattered field and ψ⁰ is the incident field. Since n = 1 in vacuum, ψ⁰ satisfies

Subtracting (3) from (1), we obtain a "scattered field form for the wave equation,"

In two-dimensions, we descretize (4) using the S-FDTD algorithm and obtain

Similarly, the NS-FDTD algorithm gives

where v₀ = ω / k₀.

Scattered Field Form for Maxwell's Equations

Maxwell's equations are given by

We separate

where H^s, E^s are scattered fields and H⁰, E⁰ are incident fields. These incident fields safisfy

where μ₀ and ε₀ are the permeability and permittivity in vacuum, respectively. Subtracting (9) from (7), we obtain a "scattered field form for Maxwell's equations,"

In two-dimensions, we discretize (10) using the S-Yee algorithm and obtain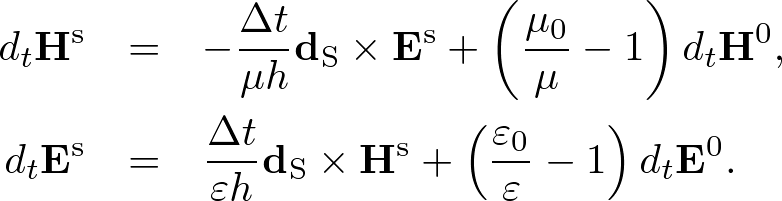

Similarly, the NS-Yee algorithm gives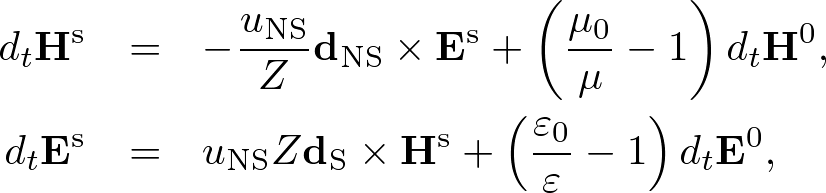

where Z = (μ/ε)^1/2 and

Copyright (C) 2011 Naoki Okada, All Rights Reserved.