Morpho Butterfly Rendering

Language

English / Japanese

Home

Nonstandard FDTD Simulations

Update History

Homepage is opened! (13 Nov. 2012)

Nano-structures of Morpho butterfly scales

The male Morpho rhetenor butterfly has subwavelength structures on its scales, as shown in Figure 1: images (a) and (b) were made using an optical microscope and (c) is a transmission electron micrograph. Figure 1 shows (a) the arrangement of scales on a wing; (b) a single scale; (c) ridges and lamellae alignments on a cross-section of the scale. The width and thickness of a lamella are about 300nm and 100nm in subwavelength regime, respectively. Figure 1(d) is a simplified perspective view of a scale, where lamellae are inclined at about 10^° to the x-z plane. The ridges are composed of staggered lamellae like a book shelf.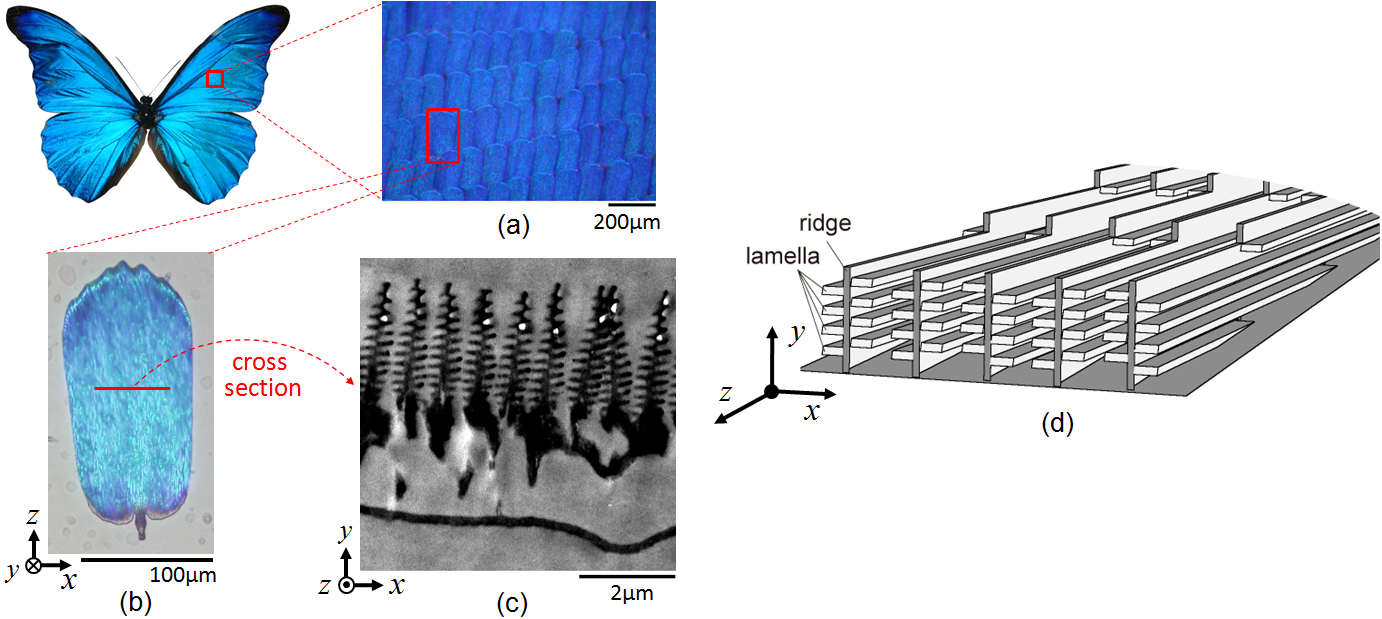

Fig. 1. Male Morpho rhetenor wing scale. (a) Arrangement of scales on the wing. (b) A single scale. (c) Ridges and lamellae alignments on the cross-section of a scale. (d) Simplified 3D depiction of the scale.

Three photonic crystal-like structures coexist in the array of ridges and lamellae. The first one is a 1-D multilayer which gives rise to the blue color. Thin films with air and lamellae can be approximated by a multilayer film structure. The reflected wavelength of a multilayer must satisfy [SM90] [JMW95] [TKF^*96].

where n is the refractive index, d is the thickness of a film, θ is the refraction angle, λ is the incident wavelength, and m is an integer. The subscripts l and a denote the lamella and air, respectively. Given typical parameters in the microscope image, n_l = 1.55, n_a = 1, d_l = 80nm and d_a = 115nm in Eq. (1) and putting m = 1, we obtain λ = 480nm (blue light) at normal incidence (θ_l = θ_a = 0).

The second photonic crystal-like structure causes blue light backscattering by the bookshelf-like staggered lamella on each ridge. A ridge is composed of a set of staggered lamella in the right and left side of ridges. The staggered lamellae on a ridge form two phase shifted photonic crystals on the left and right. These two photonic crystals interact with light in each a way that the blue component scatters back to its source [ZKCC09] [KZK11].

The third photonic crystal-like structure is a diffraction grating formed by ridges of random height. A pair of ridges can be approximated by a single slit structure. Single slit diffraction is given by

where d_r is the ridge interval and φ is the reflection angle. Taking λ = 480nm, d_r = 550nm and m = 1, we obtain a diffraction peak at φ = 60^°. Although the structure of the Morpho butterfly is periodic, its width, height, and ridge (lamella) shape contain some randomness, which randomly shifts the phases of reflected waves and cancels out the grating effect [ZKCC09].

It is said that the coexistence of these three photonic crystal-like structures is the origin of the brilliant iridescence of the Morpho butterfly. But the combination of these effects is difficult to theoretically analyze and is best solved by numerical simulations. Note that the anisotropic reflections are mainly in the x-y plane and observed by rotating the body around the z-axis as shown in Fig. 1(d). This is because many ridges uniformly extend along the z-axis.

Simulation moel of the Morpho butterfly scale

To compute the optical characteristics, we need a model of the Morpho butterfly scales. As discussed before, diffraction spots generated by slit interference are washed out by many ridges of random height. If only a few scales are used in the simulation, spurious diffraction spots (which the real butterfly does not display) are not washed out, but the greater the number of scales in the simulation the higher the computational cost. Fortunately, many ridges of random height are optically equivalent to one single averaged ridge [ZKCC09], and thus using one averaged ridge we can model the Morpho butterfly scales.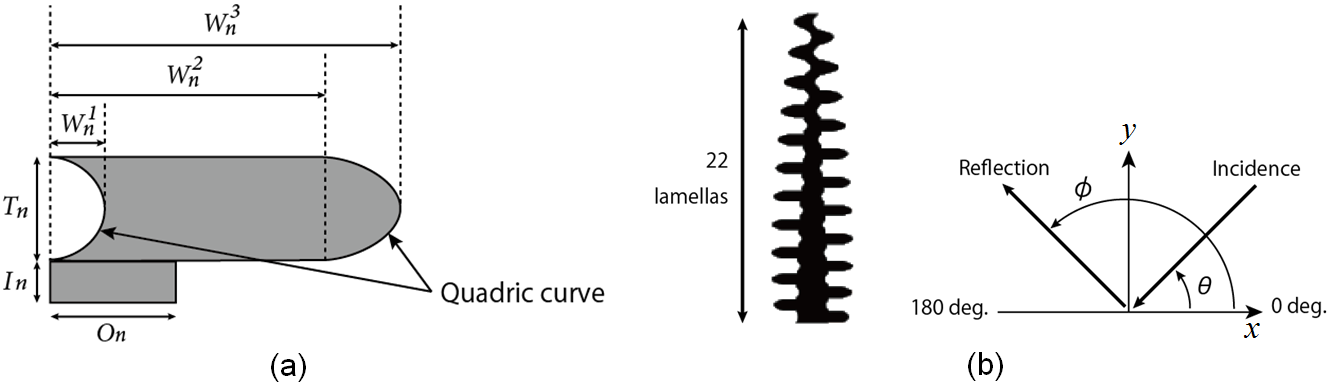

Fig. 2. A single averaged ridge that represents an entire scale in the numerical simulation. (a) Model of a single lamella on a ridge. T_n is thickness, I_n is pedestal. W₁ⁿ, W₂ⁿ, W₃ⁿ are, respectively, the widths indicated in the figure. Region O_n connects one lamella to another. (b) Single averaged ridge model (left) consisting of 22 lamellae. The incidence angle θ and reflection angle φ in x-y plane (right).

Since many ridges uniformly extend along the z-axis as shown in Fig. 1(d), the anisotropic reflection can be simply modeled on a two-dimensional x-y plane perpendicular to the wing surface. A lamella is modeled as shown in Fig. 2(a), where both ends of the lamella are approximated by a quadric curve. Averaging over a number of ridges measured in transmission electron microscope image in Fig. 1(c) and using polynomial approximations, we obtain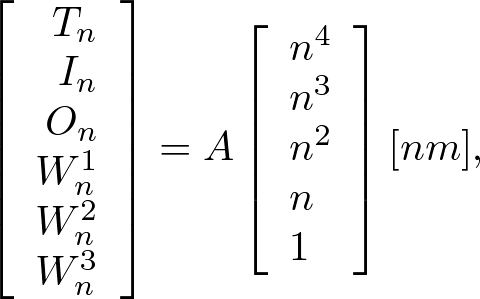

where n = 1, 2, ..., 22 is the lamella number is counted upward from the root, and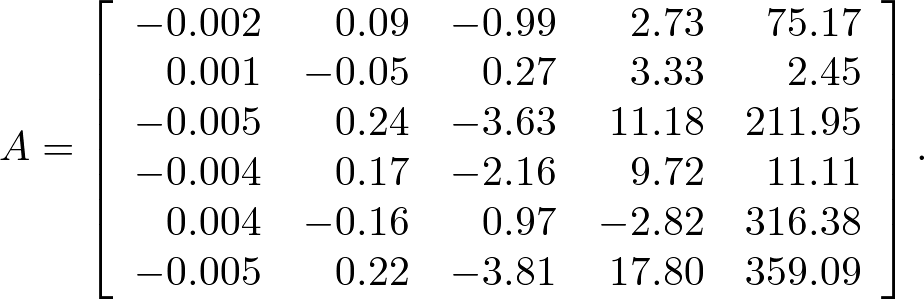

Using the above, we obtain the averaged ridge shown in Fig. 2(b). In the figure (right), the incidence angle θ and reflection angle φ are defined in the twodimensional surface with respect to this single ridge (left).

Bibliography:

• [SM90] Smits B. E., Meyer G. W.: Newton s colors: Simulating interference phenomena in realistic image synthesis. In Proceedings Eurographics Workshop on Photosimulation, Realism and Physics in Computer Graphics (1990), Eurographics, pp. 185-194.
• [JMW95] Joannopoulos J. D., Meade R. D., Winn J. N.: Photonic Crystals: Molding the Flow of Light. Princeton University Press, 1995.
• [TKF^*96] Tabata H., Kumazawa K., Funakawa M., Takimoto J., Akimoto M.: Microstructures and optical properties of scales of butterfly wings. Optical Review 3, 2 (1996), 139-145.
• [ZKCC09] Zhu D., Kinoshita S., Cai D., Cole J. B.: Investigation of structural colors in morpho butterflies using the nonstandard-finite-difference time-domain method: Effects of alternately stacked shelves and ridge density. Physical Review E, 80 (2009), 051924.
• [KZK11] Kambe M., Zhu D., Kinoshita S.: Origin of retroreflection from a wing of the morpho butterfly. Journal of the Physical Society of Japan 80, 5 (2011), 054801.

Copyright (C) 2011 Naoki Okada, All Rights Reserved.