Morpho Butterfly Rendering

言語

English / Japanese

ホーム

Nonstandard FDTD Simulations

更新履歴

ホームページ開設 (13 Nov. 2012)

シミュレーションと近傍-遠方変換

Table. 1. 計算パラメータ.

angular range	wavelength range	grid spacing	computational domain	refractive index
0 ∼ 180° (5° increments)	350 ∼ 550nm (10nm increments)	10nm	4μm × 4μm	1.55

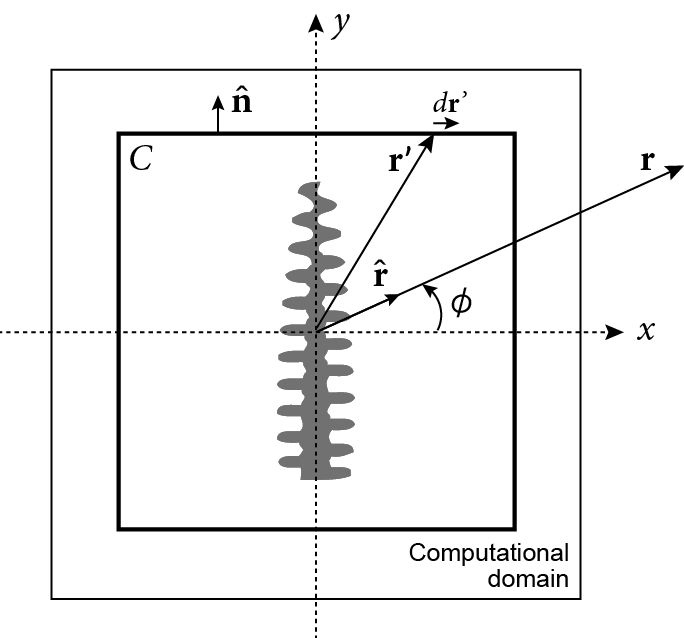Fig. 1. 近傍-遠方変換．r は遠方場の位置ベクトル, ř = r/|r|, φ は反射角, C は積分経路, r' は C 上の位置ベクトル, ň は C に直交する法線ベクトル, dr' は線素ベクトル．

まず我々は，Nonstandard FDTD法を用いてTM・TE偏光における近傍場の反射を計算する．計算パラメータを表1に示す．計算領域には，Nonstandard Perfectly Matched Layer (PML) 吸収境界条件 [OC11] を用いた．我々は通常，ナノスケールよりもずっと遠い位置からモルフォ蝶の色を観測するため，近傍-遠方変換 [LRB92] を用いて遠方場の反射率を計算する．遠方場は，図5に基づいて次式より計算される．

ここで，Z = √ (μ/ε) (μ = 透磁率, ε = 誘電率)，φ は円柱座標系の仰角. 直交座標系において，N と L は，以下のように与えられる．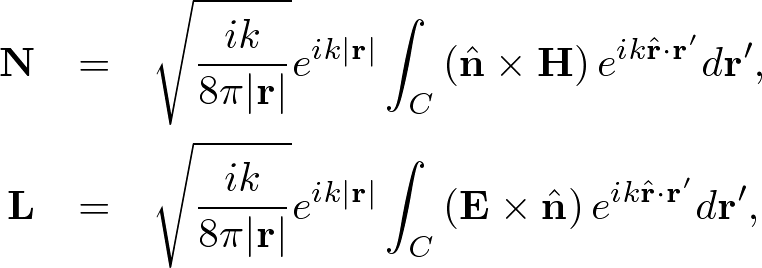

ここで，r は遠方場の位置ベクトル, ř = r/|r|, C は積分経路, r' は C 上の位置ベクトル, ň は C に垂直な法線ベクトル．N と L の円柱座標系への変換式は，

で与えられる．最終的に，遠方場の反射率 R は，次のように計算できる．

シミュレーションと実験結果の比較

全波長 λ および全入射角 θ をそれぞれ計算し，必要な反射率 R(λ, θ, φ) が得られる．この計算は，Intel Core 2 Duo 2.66GHz parallel CPU のマシンを用いて，約10時間を要した.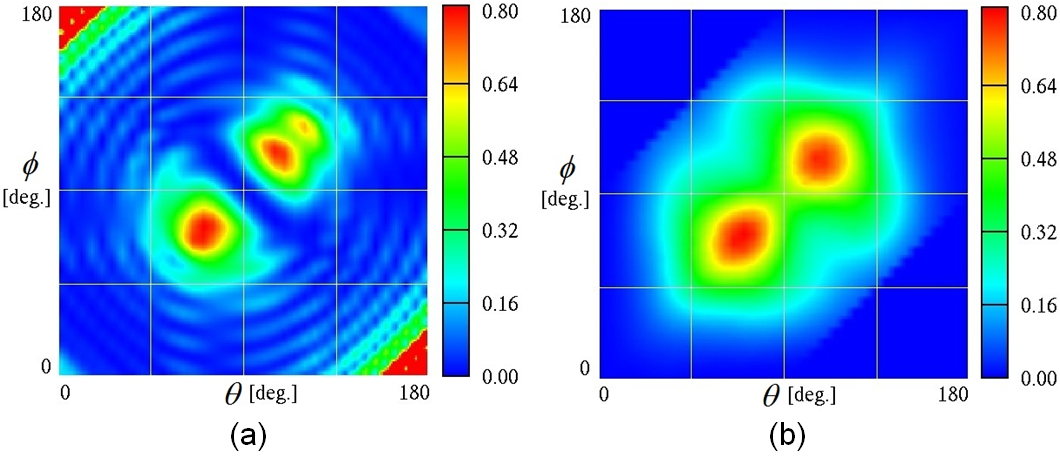

Fig. 2. 波長 = 480nm の反射率分布 (θ = 入反射, φ = 反射角). (a) 平均リッジモデルを用いた FDTD 法の計算結果．(b) 実験による計測結果 (試料は 5 × 5mm²) [KZK11].

図2(a)は，FDTDシミュレーションで計算された波長 = 480nmの反射率分布である．図2(b)は，実験による計測結果である．実験は，5 × 5mm² の試料に対して全角度反射測定法が用いられた [KZK11]. 計算結果と実験結果は，これまで利用されてきた回折モデル [KYFO02] で得ることのできない後方散乱を観測できている．計算結果にのみ透過光(図の左上と右下)が現れているが，これは単一リッジに簡単化した影響である．多数のリッジがあれば，三角形のリッジ形状により透過光は翅の裏に抜けていく．この点は，後に述べるシェーディングモデルによって影響を抑えている．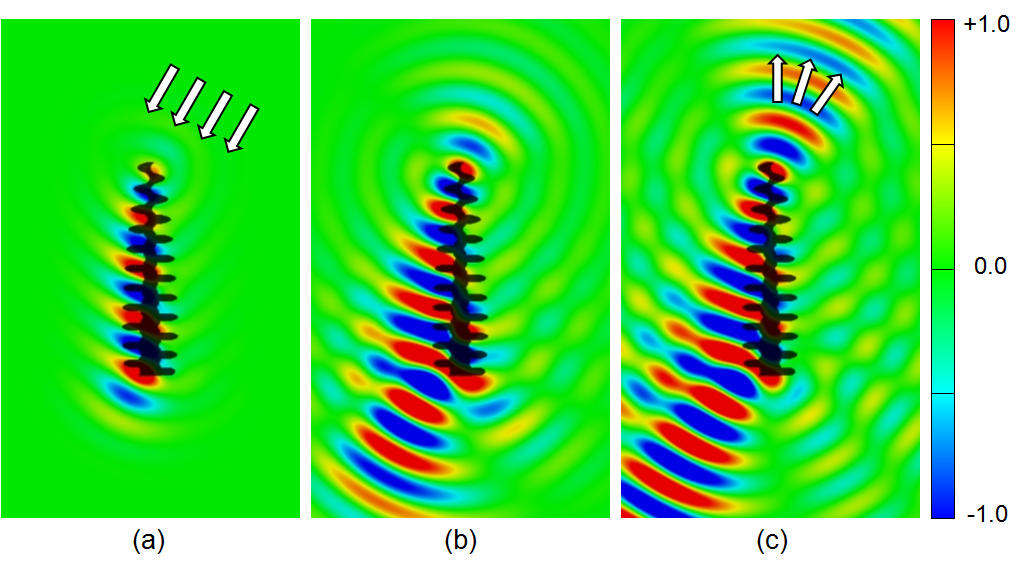

Fig. 3. TM偏光における後方散乱(波長 = 480nm)．黒い部分は，平均リッジモデルを表している．(a) θ = 75^° の平行光を与え，3周期後の散乱電場分布．(b) 6周期後の電場分布．(c) 15周期後の電場分布． Backscattering in simulation of the TM mode (wavelength = 480nm). Black region is a single averaged ridge model. (a) Parallel beam is incident at θ = 75^°, indicated by white arrows, at time = 3 wave periods. (b) Scattered waves interact with each other as they propagate along several direction at time = 6 wave periods. (c) Interference causes backscattering indicated by white arrows at time = 15 wave periods.

近傍場の解析において，後方散乱は視覚的に捉えることができる．図3は，TM偏光の平行光(波長480nm, 入射角θ = 75^°)を与えたときの散乱電場分布である．図3(a),(b),(c) は，それぞれシミュレーションを開始して，3, 6, 15 周期経過した後の分布である．図3(b)においてリッジによる散乱が現れ，図3(c)では光源方向に強い反射を観測できる．先に述べた通り，この後方散乱は互い違いの構造によってもたらされている．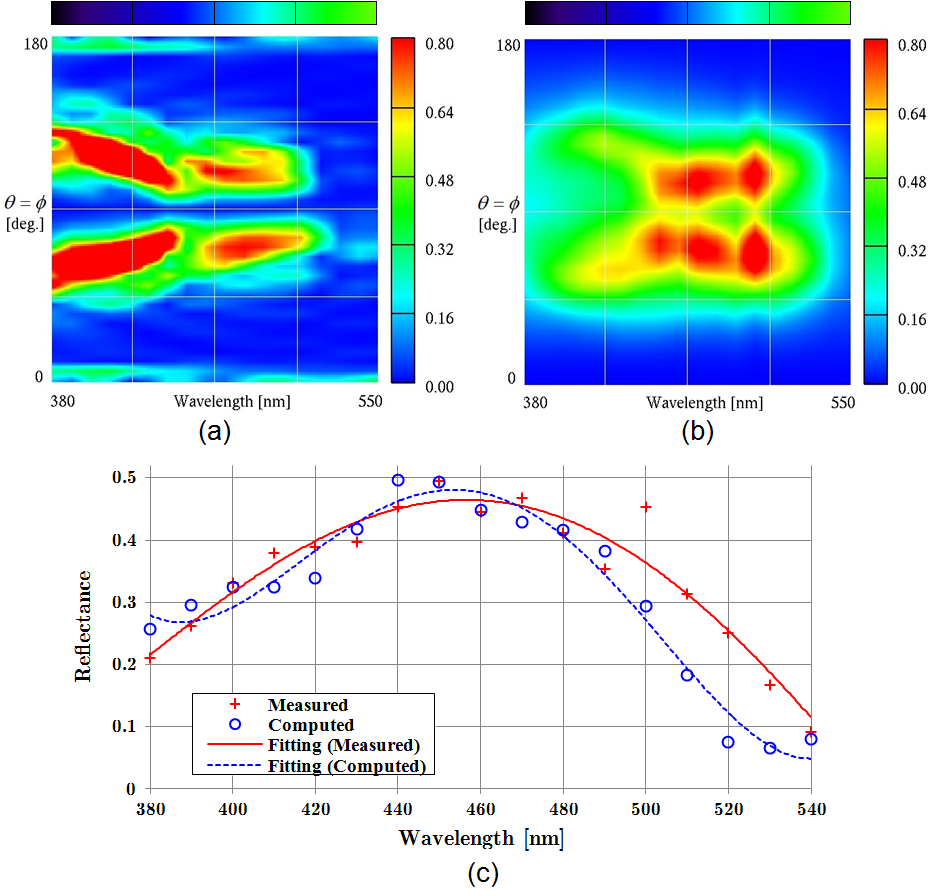

Fig. 4. 反射スペクトル．(a) 計算結果，(b) 実験結果 [KZK11] (ただし，θ = φ)．上のグラデーションは光色，右のグラデーションは反射率を示す．(c) 全方位で積分した反射スペクトル(θ = 90^°)．

ここで，反射スペクトルを実験結果 [KZK11] と比較する．図4(a)と(b)は，後方散乱軸 θ = φ に沿ったシミュレーションと実験による反射スペクトルである．図4(a), (b)において，短波長側に違いが見られる．これもまた，単一リッジに簡単化した影響であり，多数のリッジがあれば短波長ほど干渉による打ち消し効果が強い．幸いこの領域では，日光のエネルギーが弱いため，構造色への影響は小さい．図4(c)において，全方位で積分した反射スペクトル(θ = 90^°)を示す．先行研究の解析結果 [ZKCC09] [LS09] は実験結果と大きくズレているが，我々の計算結果は実験結果とより良い一致を示している．特に反射の強い460nm前後の波長では，先行研究との違いが顕著であり，再現する構造色のリアリティに大きな影響を与える．

Bibliography:

• [OC11] Okada N., Cole J. B.: A nonstandard finite difference time domain algorithm for berenger's perfectly matched layer. the Applied Computational Electromagnetic Society Journal 26, 2 (2011).
• [LRB92] Luebbers R. J., Ryan D., Beggs J.: A twodimensional time-domain near-zone to far-zone transformation. IEEE Trans. Antennas and Propag. 40, 7 (1992), 848-851.
• [KZK11] Kambe M., Zhu D., Kinoshita S.: Origin of retroreflection from a wing of the morpho butterfly. Journal of the Physical Society of Japan 80, 5 (2011), 054801.
• [KYFO02] Kinoshita S., Yoshioka S., Fujii Y., Okamoto N.: Photophysics of structural color in the morpho butterflies. Forma 17 (2002), 103-121.
• [ZKCC09] Zhu D., Kinoshita S., Cai D., Cole J. B.: Investigation of structural colors in morpho butterflies using the nonstandard-finite-difference time-domain method: Effects of alternately stacked shelves and ridge density. Physical Review E, 80 (2009), 051924.
• [LS09] Lee R. T., Smith G. S.: Detailed electromagnetic simulation for the structural color of butterfly wings. Applied Optics 48, 21 (2009), 4177.4190.

Copyright (C) 2011 Naoki Okada, All Rights Reserved.